The positional accuracy of a GPS depends on the environment it’s operating in; if six satellites are in the sky on a clear sunny day in the countryside, the positional accuracy will be high. But if there is a thunderstorm in the area with only 3 satellites in the middle of a metropolis, the positional accuracy diminishes. Pinpoint accuracy requires ideal conditions.
Similarly, a CBTC train’s ability to report an accurate position depends on the design of the train and the track it’s running on. Train parameters and track characteristics must be understood and controlled to reduce positional uncertainty; otherwise the train cannot be tracked nor can it be protected.
Positioning Basics
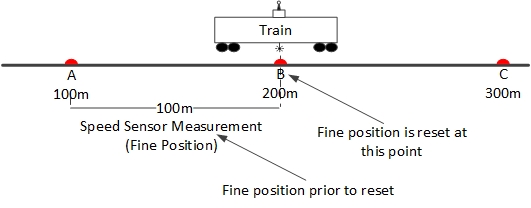
The basic premise behind a CBTC system is its ability to determine the location of a train independent of track circuits. Transponder tags or beacons (tag will be used for the remainder of the post) installed along the track provide coarse position and speed sensors installed on the axle provide fine position.
When tag A is detected, the train borne unit is aware the train is located at the 100 meter mark (coarse position), and the speed sensor counts how far away the train has moved from tag A (fine position). The train borne unit is able to calculate the position by adding the coarse and fine position together (147.5m away from the zero reference point).
When tag B is detected, the coarse position is updated to 200m and the fine position is reset to zero and the process repeats itself.
If tag B is detected and the speed sensor reports the train has moved 70m from tag A, then failure handling is invoked.
Tag B is indicating the train has travelled 200m but the speed sensor measurement is indicating the train has moved only 170m (tag A + fine position). Either the tag is installed in the wrong location or the speed sensor has failed.
What is Positional Uncertainty?
Positional uncertainty is the area of track where the train might be located. The magnitude depends on the track characteristics and train parameters.
If a train reports a position of 147.5m, the actual position may be 150m or 145m (+/- 2.5m for example). This extra 2.5 meters in front and behind the train is called the positional uncertainty and must be considered occupied.
The positional uncertainty is not static it builds as the train moves. From a signalling perspective this means the length of the train increases the further the train travels; if the train length is 150m, it becomes 150m plus the positional uncertainty. Unless the positional error is reset at regular intervals, the error will grow until it’s impossible for the signalling system to track the train.
How is Positional Uncertainty Calculated?
Several factors affect positional uncertainty and they are broken into two components, the static and dynamic uncertainty.
Static Uncertainty (S)
The static uncertainty is present from the moment the train borne unit is powered on. It’s fixed and does not change when the train moves and it’s composed of the following factors:
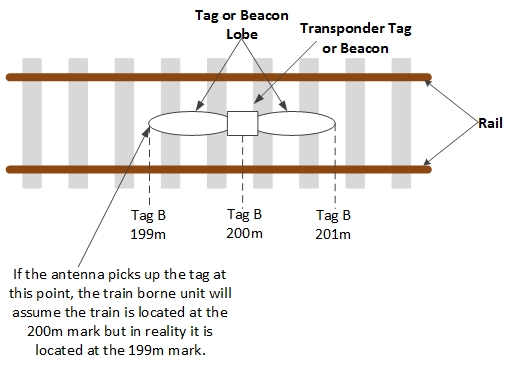
- Transponder Tag footprint –the lobes that radiate out from the tag create a footprint. When the train passes over the tag, the tag antenna (on the train) may detect the tag earlier (or later) then it should. If the tag is located at the 200m mark, the antenna may detect the lobe at the 199m mark, causing the train borne unit to assume the train is located the 200m mark when in reality, it’s located at the 199m mark.
- Transponder Tag Installation error – the location of the tags is hardcoded in the train borne unit software. When the train passes a tag, the train borne unit is aware the train is located at the 200m mark on the track. But if the tag is shifted to either side by a small margin, the train borne unit will still consider the train is located at the 200m mark but in fact the train is located 200m plus or minus the installation error.
- Train board unit precision – the train borne unit is a microprocessor operating in the digital world. The microprocessor has its own numerical error such as an overflow or an underflow which will reduce the accuracy of the position.
The static error is present at all times and it can never be reset.
Dynamic Uncertainty (D)
The dynamic uncertainty is related to train movement. It’s based on the distance the train has travelled since a known reference point; as the train moves the error increases.
The dynamic uncertainty is composed of the following factors:
- Wheel slip – if the speed sensor is installed on a powered axle, the wheel can slip when the train accelerates. This is similar to a car spinning its wheels when it accelerates suddenly; the odometer detects movement but the car did not move. Most suppliers have a mechanism to detect wheel slip but undetected micro slips around curves will not be detected.
- Wheel slide –if the speed sensor is installed on a braked axle there is a chance the axle will lock and the train will slide. From the speed sensor perspective, the train stopped but in reality it’s still moving (sliding). If a supplier does not have a mechanism in place to detect wheel slide, the dynamic uncertainty will be higher.
- Speed sensor granularity – The speed senor is a device connected to the axle of the train. It determines the speed and distance the train has travelled based on the number of pulses per revolution. This device has its own error that builds up over the distance travelled.
- Wheel calibration – the diameter of the wheel changes over time. The train must run a wheel calibration test to determine the actual wheel diameter which is used to calculate the distance the train travels every revolution. If the wheel calibration test fails, this will add to the dynamic uncertainty.
The dynamic uncertainty is reduced to a percentage of the total distance travelled from the known reference point and added on top of the distance travelled by the train front and subtracted from the rear; the percentage error varies from as low as 2% and as high as 10% depending on the supplier.
Unless there is a mechanism to reset the dynamic uncertainty, the error will grow indefinitely causing the length of the train to increase indefinitely. To control this behaviour, the tag is used to reset the dynamic error because it’s an established reference point; the installation is guaranteed within a certain margin of error. When the train detects the tag, the dynamic error is reset (but not the static error).
Put it altogether
The tag is the key component for the positioning system because it determines where the train is located plus or minus the static uncertainty.
As the train moves away from the tag, the dynamic uncertainty starts to grow and is reset only when the next tag is detected. The static portion is never reset.
If tag B is not detected, the dynamic error will continue to grow. The industry has converged on allowing the train to continue moving if one tag is missed but if a second tag (back to back) is missed the train will be forced to come to a stop; the dynamic error has reached a size where the CBTC signalling system cannot determine where the train is located.
Is Positional Uncertainty the Same Every Where?
Tag placement determines the magnitude of positional uncertainty; the closer the tags, the smaller the positional uncertainty. Therefore, it is logical to assume the tags are placed at regular intervals (for example 35m) along the track but, the suppliers have not taken this approach.
Positional uncertainty is important when the train has to align at the platform where the stopping accuracy is between +/-25cm to +/- 50cm. But in between the stations the system can handle a positional uncertainty of +/-10m to +/-100m.
The general rule is, the tags are spaced out one to two hundred meters in between the stations and as close as 10 meters apart leading into the station stopping point.
Accurate positioning is the heart of any CBTC system and therefore the factors that affect positional accuracy must be understood and controlled.
A measure of a suppliers CBTC solution is to ask what their worst case positional uncertainty is. It is a mark of the supplier’s mastery over their CBTC solution when the positional uncertainty is reduced to the smallest value possible.